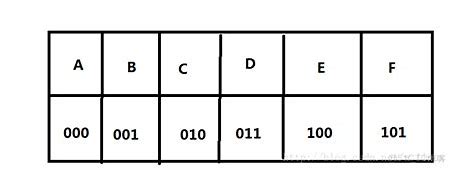
哈夫曼编码正确性的证明
...
背包问题
背包问题问题描述给定一组物品,每种物品都有自己的重量和价值,背包的容量为 W,如何选择物品,使得背包中物品的总价值最大? 问题分析这是一个典型的动态规划问题,我们可以用二维数组 dp[i][j] 表示前 i 个物品恰好装入一个容量为 j 的背包可以获得的最大价值。v[i] 表示第 i 个物品的价值,w[i] 表示第 i 个物品的重量。 边界条件:dp[i][j] = 0,i=0 or j=0。 状态转移方程如下: 1dp[i][j] = max(dp[i-1][j], dp[i-1][j-w[i]] + v[i]) 解释: 如果不放第 i 个物品,那么前 i-1 个物品恰好装入一个容量为 j 的背包可以获得的最大价值是 dp[i-1][j]; 如果放第 i 个物品,那么前 i-1 个物品恰好装入一个容量为 j-w[i] 的背包可以获得的最大价值是 dp[i-1][j-w[i]],加上第 i 个物品的价值 v[i] 就是第 i 个物品恰好装入一个容量为 j 的背包可以获得的最大价值。 代码实现12345678910def...